Module 3: Understanding the resting potential#
The resting potential of a neuron is the electrical potential difference/voltage across the plasma membrane at which the neuron is in a non-excited state (i.e., neither sending nor receiving any signal). [1] Understanding the resting potential is crucial for grasping how neurons remain ready to fire an action potential and how they process and transmit information. However, before delving into this topic, it is important to first explore the electrical properties of neurons, as electricity is the primary means by which neurons communicate.
3.1 Fundamentals of electricity#
Let’s review some fundamental concepts of electricity that will help us explore the electrical properties of neurons.
3.1.1 Current#
It is defined as the rate of flow of charge. In neurons, it is the movement of ions like sodium (Na+), potassium (K+), Chloride (Cl-), and Calcium (Ca2+) across the membrane, which is essential for generating electrical signals.
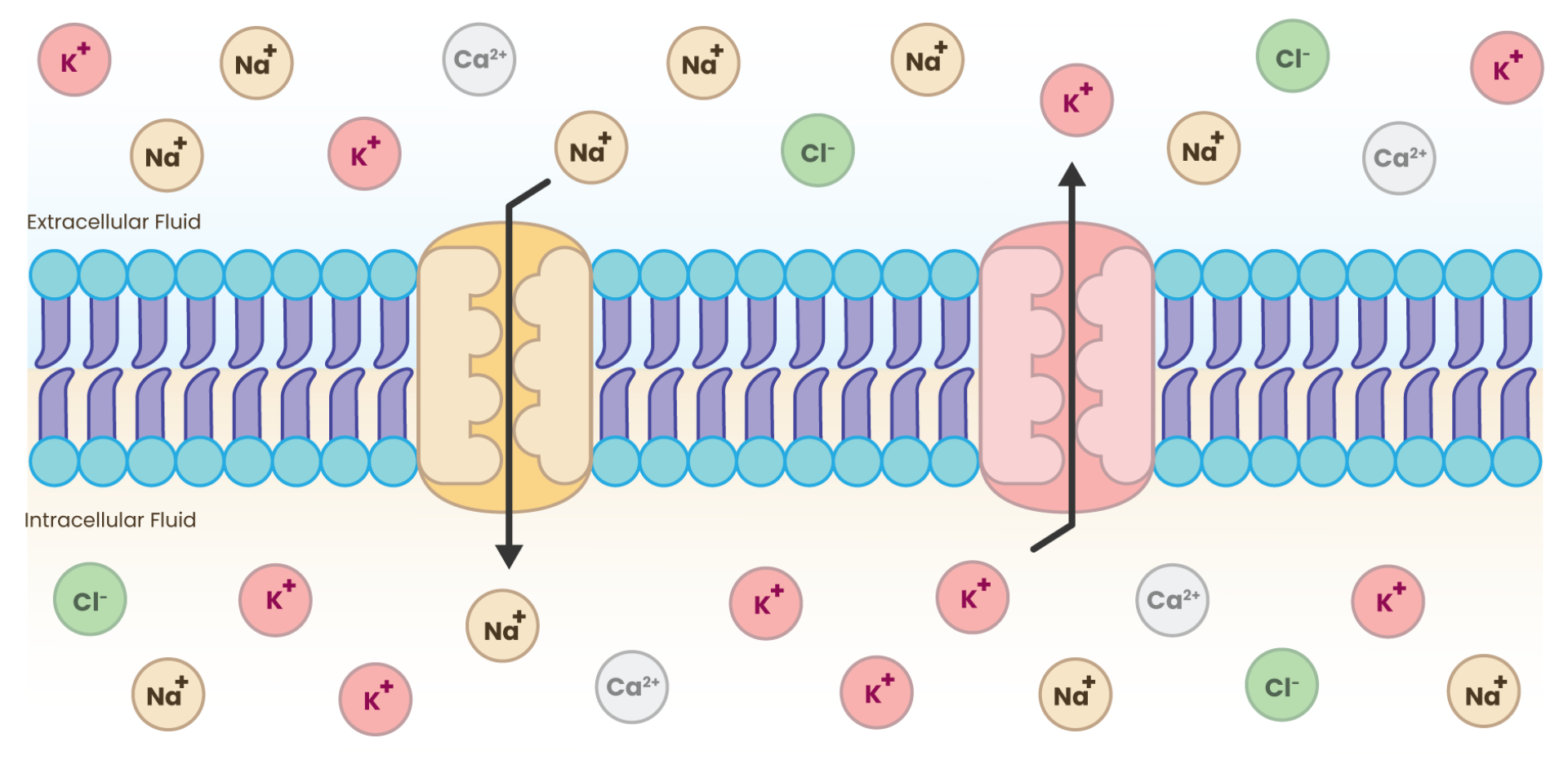
Current: The movement of ions across the membrane#
3.1.2 Voltage#
It is the electrical potential that drives the flow of charge which was discovered by Alessandro Volta in 1778. In the context of neurons, voltage refers to the electric potential difference across the neuron’s membrane, which is critical for generating and transmitting electrical signals.
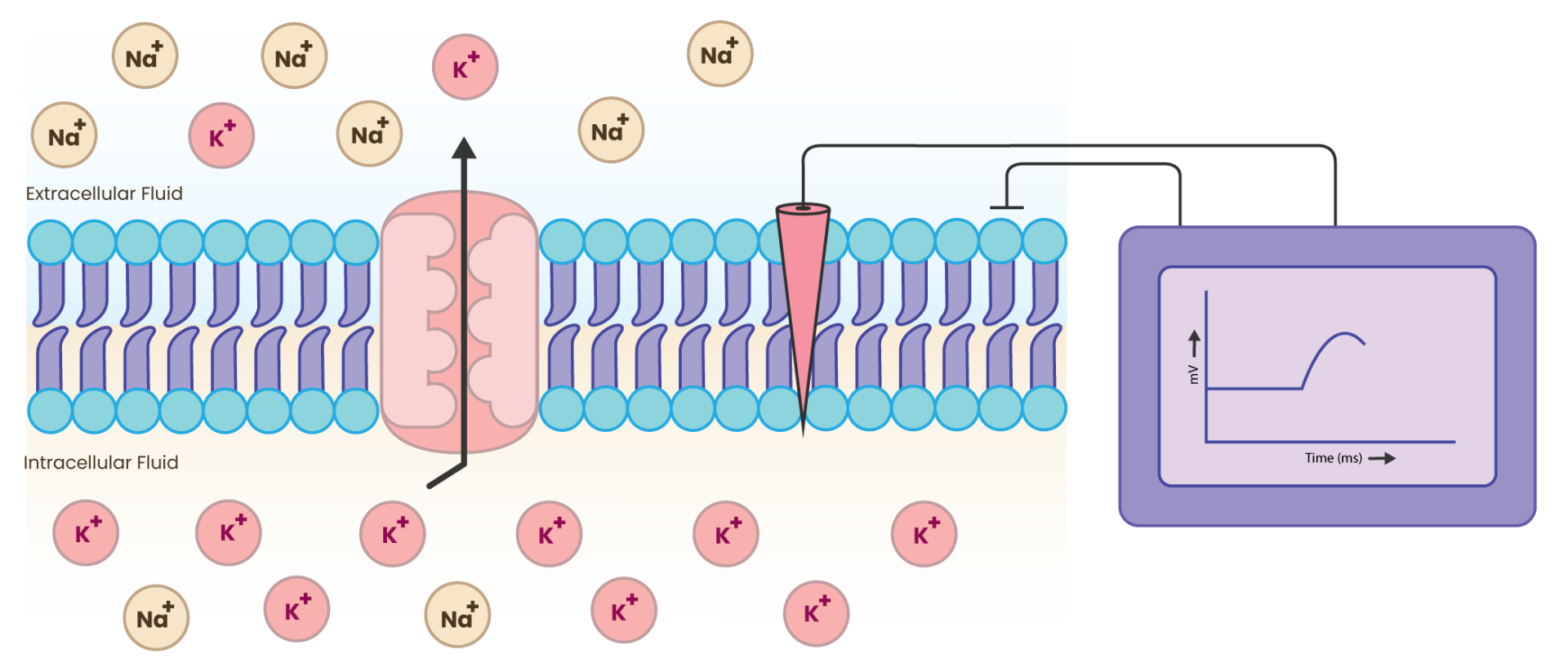
Voltage: electric potential difference across the neuron’s membrane#
To better understand electric potential, it’s essential to define electrostatic force.
3.1.3 Electrostatic force#
It is the force that arises due to the interaction between charged objects or particles. These forces are part of the fundamental forces of nature and are described by Coulomb’s law.
Electrostatic force#
3.1.4 Coulomb’s law#
The electrostatic force (F) between two point charges (q1 and q2) is given by:
Equation 1:
F = Electrostatic force
k = Coulomb constant (8.99×10*9 Nm*2/C*2)
q1,q2 = charges
r = distance between the centers of the two charges
Additional info
Coulomb’s law was first published in 1785 by French physicist Charles-Augustin de Coulomb.
3.1.5 Law of attraction & repulsion#
Attractive force: If the charges are of opposite signs (positive and negative), the force is attractive in nature.

Attractive force#
Repulsive Force: If the charges are of the same signs (both positive or both negative), the force is repulsive in nature.
Repulsive force#
3.2 Resting Potential#
Resting potential refers to the electrical potential difference across the neuron’s membrane when a neuron is at rest. It is primarily determined by the unequal distribution of ions, particularly potassium (K+) and sodium (Na+), across the neuron’s membrane. [1]
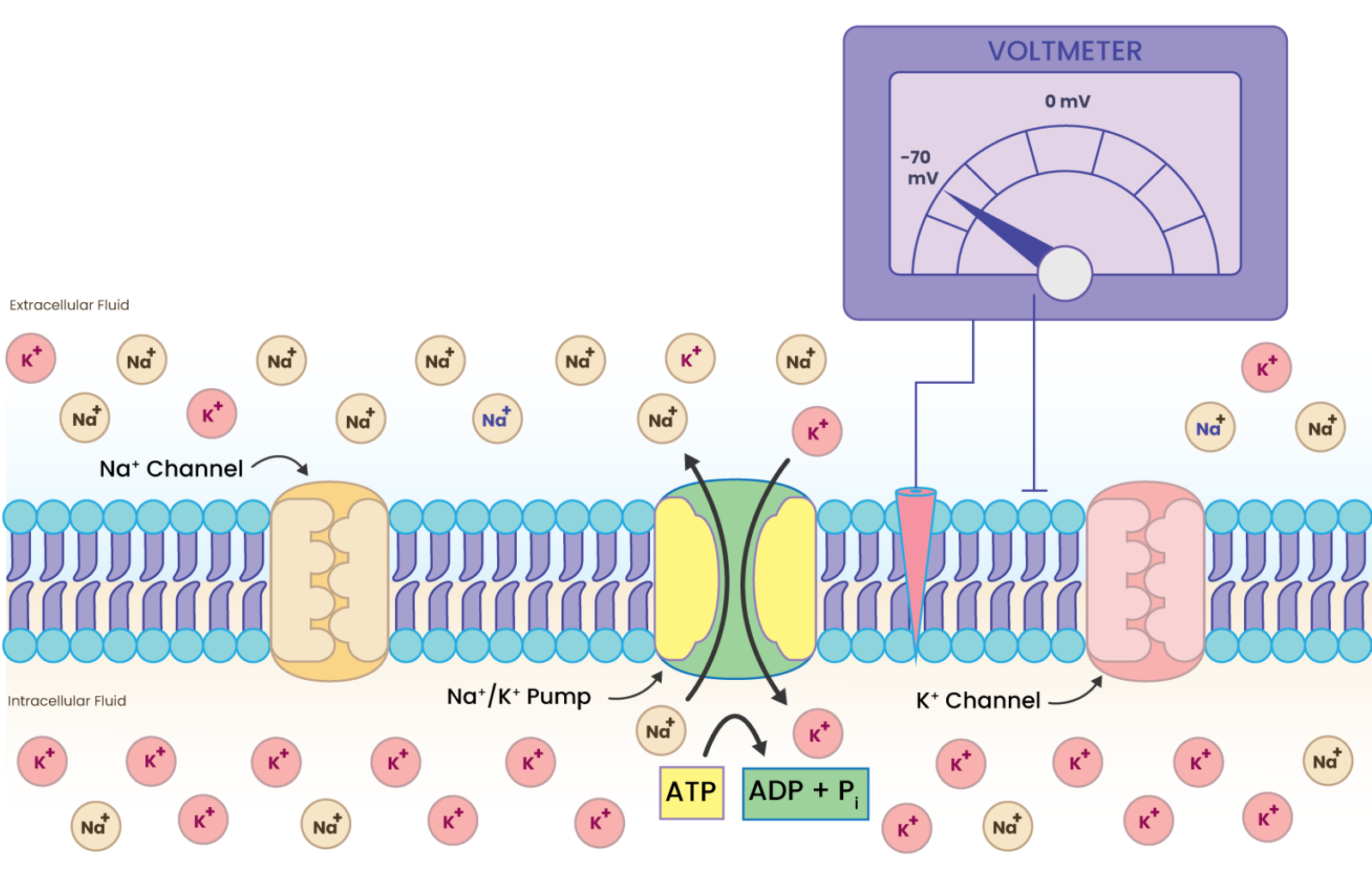
Resting potential#
Note
Membrane potential is the voltage across the membrane at any given moment, whereas resting potential is the membrane potential when a neuron is at rest (i.e., neither sending nor receiving any signal).
- The voltage across a membrane is a comparative measurement. Neuroscientists consistently use the outside of the cell as the reference point for measuring the voltage across the membrane. For instance, if the inside of the cell is 70 mV more negative than the outside, we would express the voltage as -70 mV. [1]
Voltage range of membrane potential : -60 mV TO +90 mV
Voltage of resting potential: Approx -70 mV
The resting potential of a neuron is primarily influenced by two key factors: diffusion and electrostatic forces. Let’s understand them individually. [1]
3.2.1 Diffusion [1]#
Ion Concentration Gradients#
Neurons maintain specific concentrations of ions, particularly sodium (Na+), potassium (K+), chloride (Cl-), and organic anions (A⁻), across their membrane. Typically, there is a higher concentration of K+ inside the neuron and a higher concentration of Na+ outside.
Movement of Ions#
Due to the concentration gradient, ions tend to move from areas of higher concentration to lower concentration through channels in the neuron’s membrane. For example, K+ ions diffuse out of the neuron, while Na+ ions tend to diffuse into the neuron.
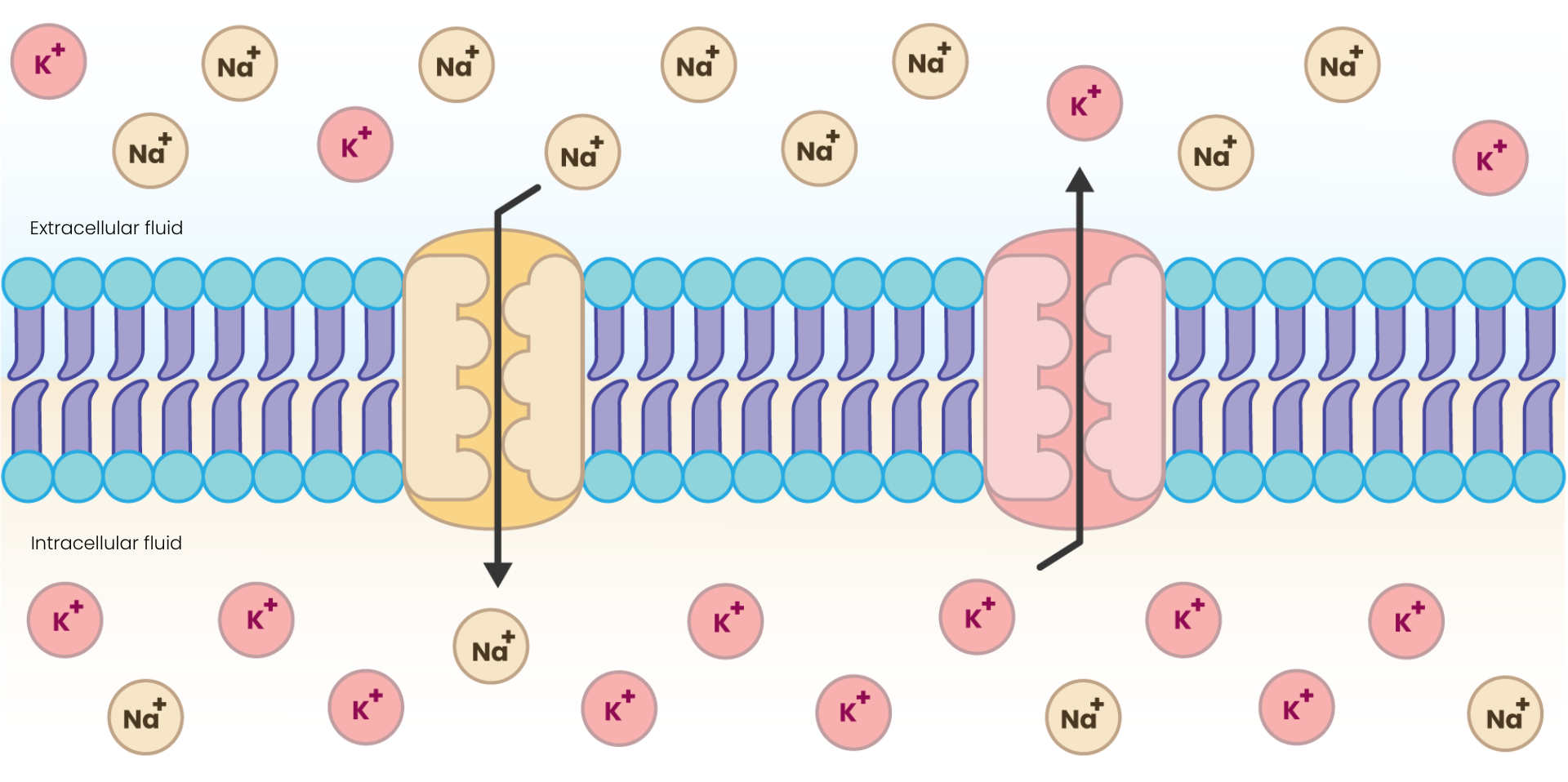
Diffusion of ions#
3.2.2 Electrostatic forces [1]#
Electrostatic forces are essential in creating the resting potential of neurons. It arises from the movement of ions like potassium and sodium, which are influenced by concentration gradients and the attractive/repulsive forces between charged particles. The unequal distribution of these ions across the membrane, combined with electrostatic forces, results in a negative charge inside the neuron relative to the outside, leading to a typical resting potential of around -70mV, which is crucial for the neuron’s ability to generate action potentials and communicate with other neurons.
3.3 Equilibrium potential#
The equilibrium potential (also known as the Nernst potential) for a specific ion is the membrane potential at which the net flow of that ion across the membrane is zero. At this potential, the concentration gradient (diffusive forces) is balanced by the electrical gradient (electrostatic forces). This means that the electrostatic forces pulling the ion into the cell are exactly balanced by the concentration gradient pushing it out (or vice versa). [1]
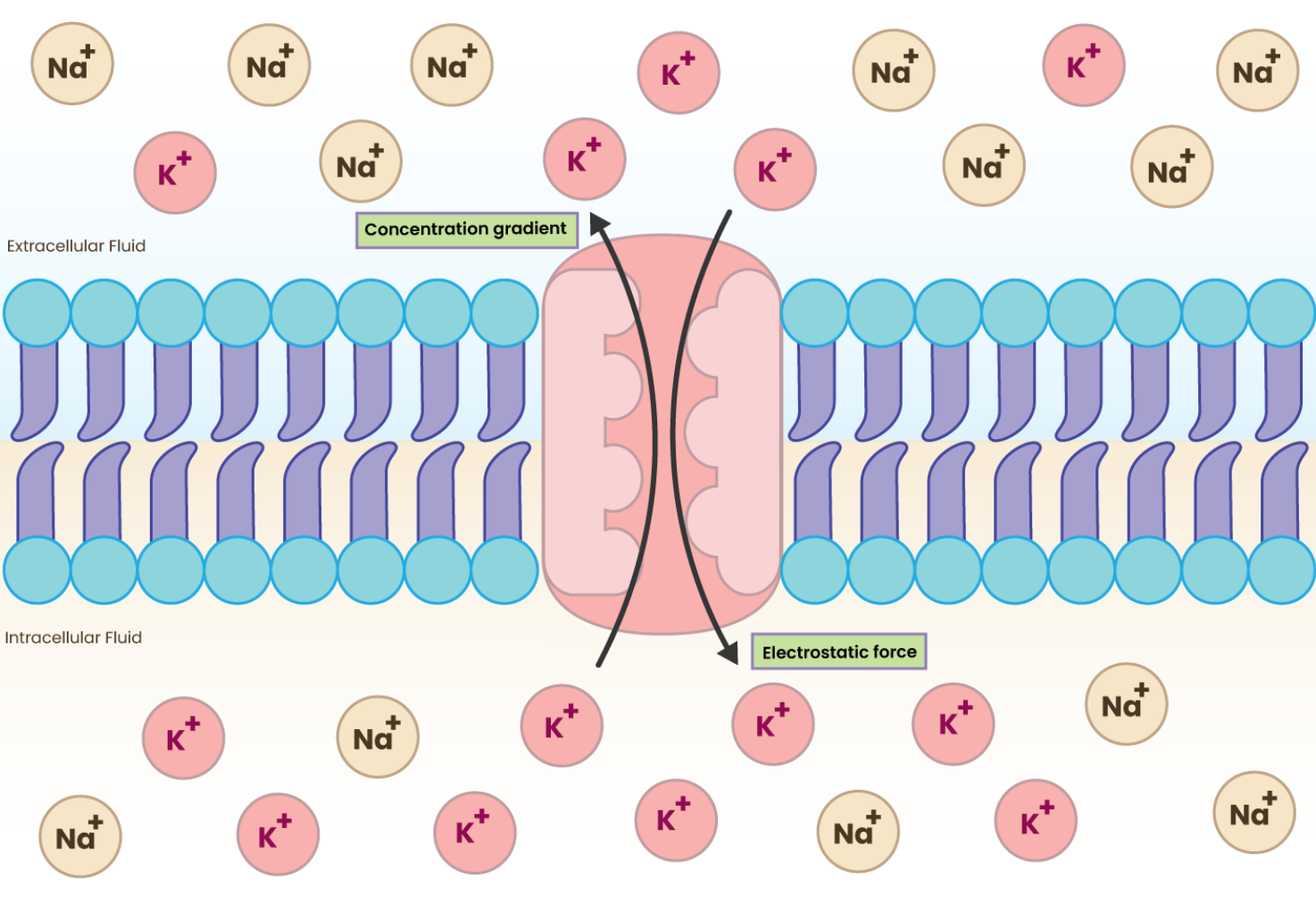
Equilibrium potential#
Nernst Equation: The equilibrium potential for a specific ion can be calculated using the Nernst equation: [2]
Where:
Eion is the equilibrium potential for the ion.
R is the universal gas constant.
T is the absolute temperature in Kelvin.
z is the valence (charge) of the ion.
F is Faraday’s constant.
Iout and Iin are the concentrations of the ion outside and inside the cell, respectively.
Equilibrium Potentials for major ions: [1]
K+: Approximately -90 mV (when K+ has an intracellular concentration of 120 mM and an extracellular concentration of 4 mM)
Na+: Approximately +60 mV (when Na+ has an intracellular concentration of 14 mM and an extracellular concentration of 140 mM)
3.4 Goldman Equation [3]#
The Goldman equation, often referred to as the GHK equation, calculates the resting potential of a cell based on the permeability and concentrations of multiple ions. It accounts for the relative contributions of different ions to the resting potential. The equation is as follows:
where:
Vm is the membrane potential
R is Universal gas constant
T is absolute temperature in Kelvin
F is Faraday’s constant
PX is permeability of ion X
Xin is concentration of ion X inside the cell
Xout is concentration of ion X outside the cell
Note
The Nernst potential (or equilibrium potential) indicates the voltage for a specific ion, but since the resting potential is affected by multiple ions, we use the Goldman equation to calculate the overall resting potential of the cell. [1]
3.5 Ion channels#
Ion channels (also called ion filters or ion-selective channels) are special proteins in nerve cells (neurons) that control the movement of ions across the cell membrane. [4] These channels help certain ions — like sodium (Na+), potassium (K+), calcium (Ca2+), or chloride (Cl-) — move quickly across the membrane based on concentration gradient (i.e. from high to low concentration). [5]
There are majorly two types of ion channels:
Leak Channels#
These are mostly open, letting ions flow freely based on their concentration gradient.
Voltage-Gated Channels#
These channels open and close in response to changes in the cell membrane potential. They are important for generating and transmitting electrical signals, like action potentials.
Ion channels are very selective, which means they only let certain ions pass through while blocking others. For instance, potassium channels allow only potassium ions (K+) to pass through while blocking all other ions. Similarly, sodium channels allow only sodium ions to pass through while blocking all other ions.
How does this work?#
You might think that an ion channel could block all positive ions by adding a positive charge to its opening, but this wouldn’t work because both K+ and Na+ are positively charged. Instead, these ion channels select ions based on their size. Sodium ions are smaller (116 picometers), while potassium ions are a bit larger (152 picometers). Still, sodium can pass through sodium ion channels and not potassium channels.
What could be the reason? Let’s see.
In neurons, sodium (Na+) and potassium (K+) ions are surrounded by a “hydration shell,” which refers to the structure of water molecules organized around each ion due to electrostatic interactions. The hydration shell for sodium ions is stronger than potassium ions due to their high charge density (i.e., charge per unit area).
What happens when both ions try to pass through the sodium ion channel? [6]
The arrangement of amino acids in the sodium ion channel favors sodium ions passage but not potassium ions . When both ions come to pass the ion channel along with their hydration shell, the arrangement of amino acids in the sodium ion channel repels and removes the sodium ion from its hydration shell but is unable to remove the potassium ion from its hydration shell. That’s why sodium ions only pass through sodium ion channels.
Similarly potassium ions only pass through potassium ion channels.
3.6 Sodium potassium pump#
The sodium-potassium pump (Na+/K+ ATPase) is a crucial membrane protein that helps maintain the proper balance of sodium (Na+) and potassium (K+) ions across the cell membrane, particularly in neurons. [7]
It is responsible for the active transport of Na+ and K+ ions, which are vital for maintaining the resting potential. This is an energy-dependent process, and the sodium-potassium pump uses energy generated by the hydrolysis of ATP into ADP + Pi to move Na+ and K+ ions against their natural concentration gradients (i.e., from high to low concentration). [8]
where:
ATP is Adenosine triphosphate
ADP is Adenosine diphosphate
Pi is the phosphate ion
Note
Active Transport is a process that involves the movement of molecules from a region of lower concentration to an area of higher concentration against their natural concentration gradient. [9]
Function of the Sodium-Potassium Pump#
Typically there is a higher concentration of sodium outside the cell and higher concentration of potassium ions inside the cell.
With every cycle, the sodium-potassium pump moves 3 Na+ ions out of the neuron and 2 K+ ions into the neuron. This results in a net export of positive charge from the neuron, contributing to the negative resting membrane potential. [7]
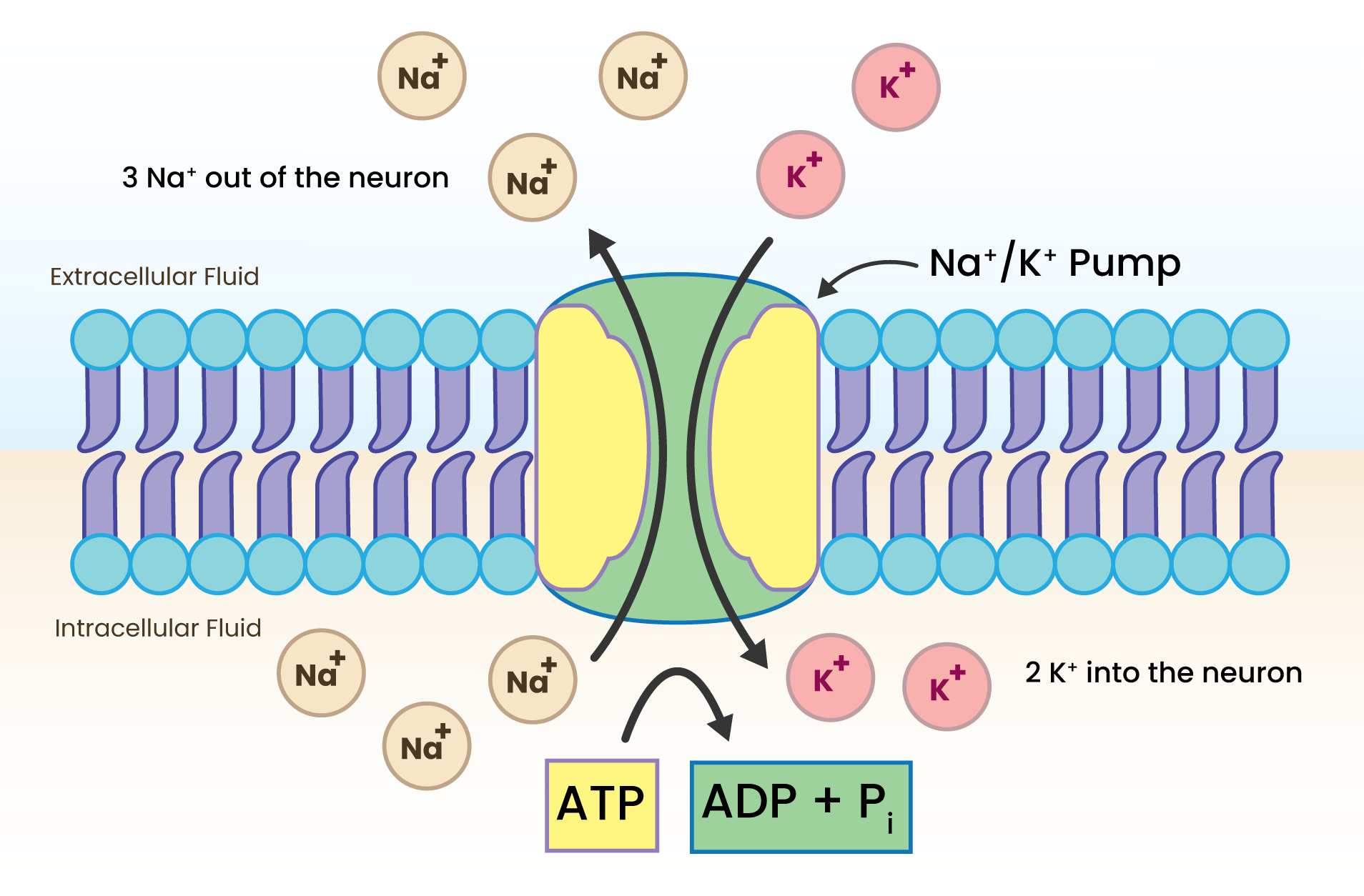
Sodium-Potassium Pump#
Note
The pump helps maintain the electrochemical gradient essential for the resting potential, typically around -70 mV in neurons. This gradient is crucial for the generation of action potentials. [10]
The action potential is a rapid, transient change in the electrical potential across a neuron’s membrane that allows it to transmit signals along its axon. It is the fundamental mechanism by which neurons communicate with one another and other cells.
Fun fact
The sodium-potassium pump consumes approximately 70% (2/3rd) energy of the nerve cell. [11]
References